用Python实现经典传染病模型

吃什么话梅 · 发表于 2022-12-11 07:55:05

2月5日凌晨更新了SEIRS模型。
<hr/>今天是2020年1月27日。根据国家卫生健康委的数据，截至2020年1月26日24时，中国30个省（区、市）累积报告确诊病例2744例，重症病例461例，累计死亡病例80例，累计治愈出院51例，疑似病例5794例，累计追踪密切接触者32799人，当日解除医学观察583人，现有30453人正在接受医学观察。
随着1月23日武汉市宣布全面封城后，各地确诊病例不断出现，2020年的新年因为新型冠状病毒（2019-nCoV）的传播而黯然失色。
本文尝试使用python对经典传染病模型进行实现，因传染病模型研究属于传染病动力学研究方向，不是本人的工作范围，因此，本人只是将模型中的微分方程，用Python进行实现，想起到抛砖引玉的效果。

（具体各个模型的理论细节，请移步其他文章）
模型一：SI-Model
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt

# N为人群总数
N = 10000
# β为传染率系数
beta = 0.25
# gamma为恢复率系数
gamma = 0
# I_0为感染者的初始人数
I_0 = 1
# S_0为易感者的初始人数
S_0 = N - I_0
# T为传播时间
T = 150

# INI为初始状态下的数组
INI = (S_0,I_0)

def funcSI(inivalue,_):
Y = np.zeros(2)
X = inivalue
# 易感个体变化
Y[0] = - (beta * X[0] * X[1]) / N + gamma * X[1]
# 感染个体变化
Y[1] = (beta * X[0] * X[1]) / N - gamma * X[1]
return Y

T_range = np.arange(0,T + 1)

RES = spi.odeint(funcSI,INI,T_range)

plt.plot(RES[:,0],color = &#39;darkblue&#39;,label = &#39;Susceptible&#39;,marker = &#39;.&#39;)
plt.plot(RES[:,1],color = &#39;red&#39;,label = &#39;Infection&#39;,marker = &#39;.&#39;)
plt.title(&#39;SI Model&#39;)
plt.legend()
plt.xlabel(&#39;Day&#39;)
plt.ylabel(&#39;Number&#39;)
plt.show()

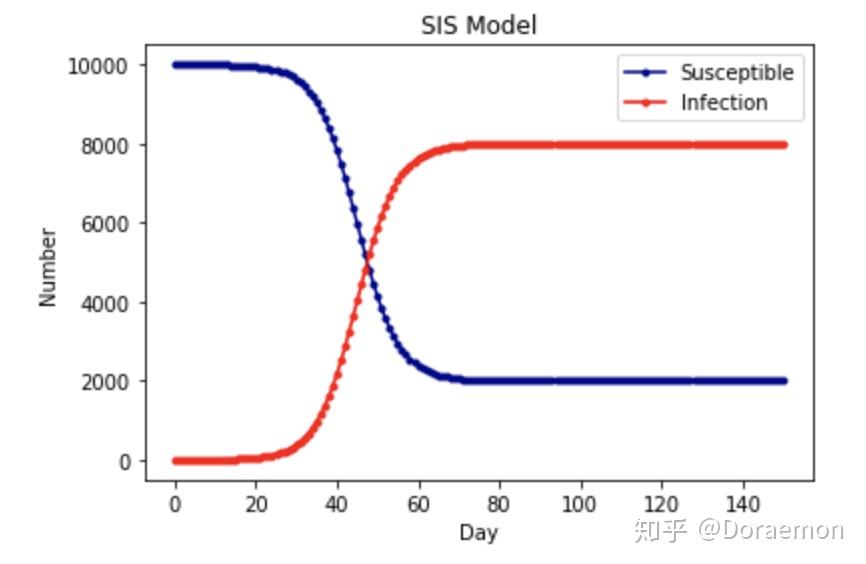
模型二：SIS-Model
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt

# N为人群总数
N = 10000
# β为传染率系数
beta = 0.25
# gamma为恢复率系数
gamma = 0.05
# I_0为感染者的初始人数
I_0 = 1
# S_0为易感者的初始人数
S_0 = N - I_0
# T为传播时间
T = 150

# INI为初始状态下的数组
INI = (S_0,I_0)

def funcSIS(inivalue,_):
Y = np.zeros(2)
X = inivalue
# 易感个体变化
Y[0] = - (beta * X[0]) / N * X[1] + gamma * X[1]
# 感染个体变化
Y[1] = (beta * X[0] * X[1]) / N - gamma * X[1]
return Y

T_range = np.arange(0,T + 1)

RES = spi.odeint(funcSIS,INI,T_range)

plt.plot(RES[:,0],color = &#39;darkblue&#39;,label = &#39;Susceptible&#39;,marker = &#39;.&#39;)
plt.plot(RES[:,1],color = &#39;red&#39;,label = &#39;Infection&#39;,marker = &#39;.&#39;)
plt.title(&#39;SIS Model&#39;)
plt.legend()
plt.xlabel(&#39;Day&#39;)
plt.ylabel(&#39;Number&#39;)
plt.show()

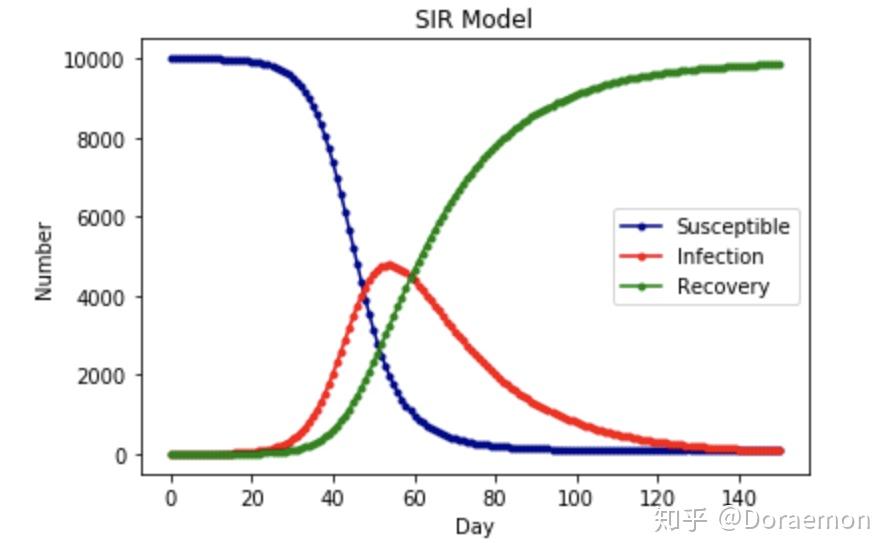
模型三：SIR-Model
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt

# N为人群总数
N = 10000
# β为传染率系数
beta = 0.25
# gamma为恢复率系数
gamma = 0.05
# I_0为感染者的初始人数
I_0 = 1
# R_0为治愈者的初始人数
R_0 = 0
# S_0为易感者的初始人数
S_0 = N - I_0 - R_0
# T为传播时间
T = 150

# INI为初始状态下的数组
INI = (S_0,I_0,R_0)

def funcSIR(inivalue,_):
Y = np.zeros(3)
X = inivalue
# 易感个体变化
Y[0] = - (beta * X[0] * X[1]) / N
# 感染个体变化
Y[1] = (beta * X[0] * X[1]) / N - gamma * X[1]
# 治愈个体变化
Y[2] = gamma * X[1]
return Y

T_range = np.arange(0,T + 1)

RES = spi.odeint(funcSIR,INI,T_range)

plt.plot(RES[:,0],color = &#39;darkblue&#39;,label = &#39;Susceptible&#39;,marker = &#39;.&#39;)
plt.plot(RES[:,1],color = &#39;red&#39;,label = &#39;Infection&#39;,marker = &#39;.&#39;)
plt.plot(RES[:,2],color = &#39;green&#39;,label = &#39;Recovery&#39;,marker = &#39;.&#39;)
plt.title(&#39;SIR Model&#39;)
plt.legend()
plt.xlabel(&#39;Day&#39;)
plt.ylabel(&#39;Number&#39;)
plt.show()

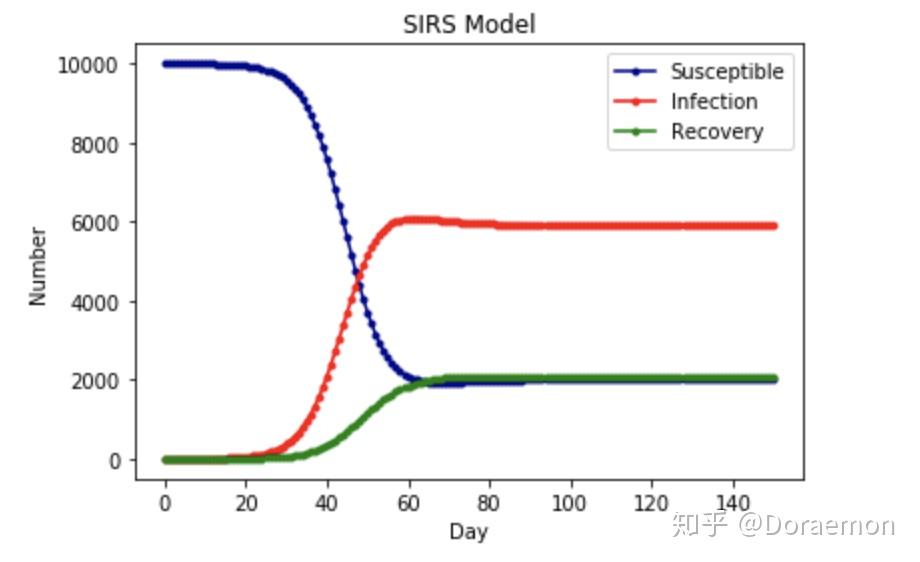
模型四：SIRS-Model
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt

# N为人群总数
N = 10000
# β为传染率系数
beta = 0.25
# gamma为恢复率系数
gamma = 0.05
# Ts为抗体持续时间
Ts = 7
# I_0为感染者的初始人数
I_0 = 1
# R_0为治愈者的初始人数
R_0 = 0
# S_0为易感者的初始人数
S_0 = N - I_0 - R_0
# T为传播时间
T = 150

# INI为初始状态下的数组
INI = (S_0,I_0,R_0)

def funcSIRS(inivalue,_):
Y = np.zeros(3)
X = inivalue
# 易感个体变化
Y[0] = - (beta * X[0] * X[1]) / N + X[2] / Ts
# 感染个体变化
Y[1] = (beta * X[0] * X[1]) / N - gamma * X[1]
# 治愈个体变化
Y[2] = gamma * X[1] - X[2] / Ts
return Y

T_range = np.arange(0,T + 1)

RES = spi.odeint(funcSIRS,INI,T_range)

plt.plot(RES[:,0],color = &#39;darkblue&#39;,label = &#39;Susceptible&#39;,marker = &#39;.&#39;)
plt.plot(RES[:,1],color = &#39;red&#39;,label = &#39;Infection&#39;,marker = &#39;.&#39;)
plt.plot(RES[:,2],color = &#39;green&#39;,label = &#39;Recovery&#39;,marker = &#39;.&#39;)
plt.title(&#39;SIRS Model&#39;)
plt.legend()
plt.xlabel(&#39;Day&#39;)
plt.ylabel(&#39;Number&#39;)
plt.show()

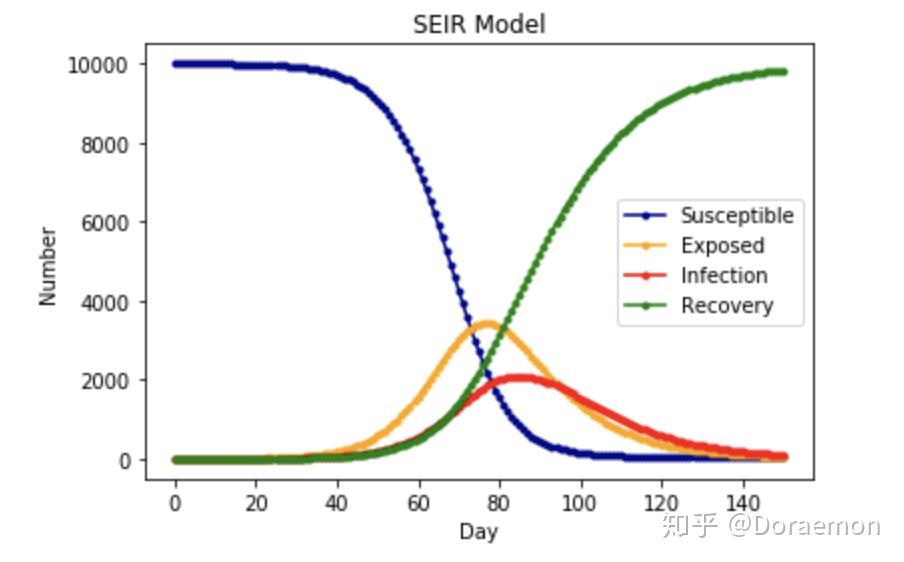
模型五：SEIR-Model
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt

# N为人群总数
N = 10000
# β为传染率系数
beta = 0.6
# gamma为恢复率系数
gamma = 0.1
# Te为疾病潜伏期
Te = 14
# I_0为感染者的初始人数
I_0 = 1
# E_0为潜伏者的初始人数
E_0 = 0
# R_0为治愈者的初始人数
R_0 = 0
# S_0为易感者的初始人数
S_0 = N - I_0 - E_0 - R_0
# T为传播时间
T = 150

# INI为初始状态下的数组
INI = (S_0,E_0,I_0,R_0)

def funcSEIR(inivalue,_):
Y = np.zeros(4)
X = inivalue
# 易感个体变化
Y[0] = - (beta * X[0] * X[2]) / N
# 潜伏个体变化
Y[1] = (beta * X[0] * X[2]) / N - X[1] / Te
# 感染个体变化
Y[2] = X[1] / Te - gamma * X[2]
# 治愈个体变化
Y[3] = gamma * X[2]
return Y

T_range = np.arange(0,T + 1)

RES = spi.odeint(funcSEIR,INI,T_range)

plt.plot(RES[:,0],color = &#39;darkblue&#39;,label = &#39;Susceptible&#39;,marker = &#39;.&#39;)
plt.plot(RES[:,1],color = &#39;orange&#39;,label = &#39;Exposed&#39;,marker = &#39;.&#39;)
plt.plot(RES[:,2],color = &#39;red&#39;,label = &#39;Infection&#39;,marker = &#39;.&#39;)
plt.plot(RES[:,3],color = &#39;green&#39;,label = &#39;Recovery&#39;,marker = &#39;.&#39;)

plt.title(&#39;SEIR Model&#39;)
plt.legend()
plt.xlabel(&#39;Day&#39;)
plt.ylabel(&#39;Number&#39;)
plt.show()

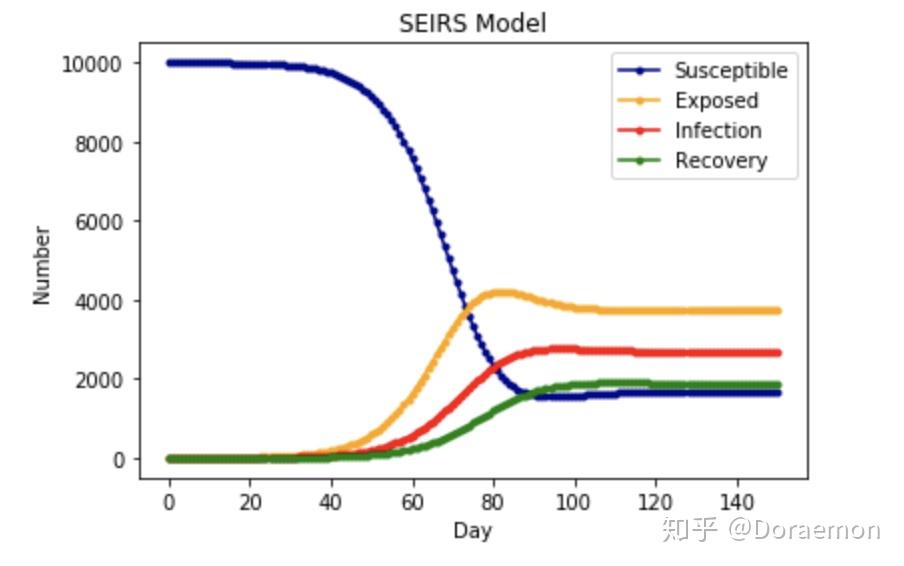
模型六：SEIRS-Model
import scipy.integrate as spi
import numpy as np
import matplotlib.pyplot as plt

# N为人群总数
N = 10000
# β为传染率系数
beta = 0.6
# gamma为恢复率系数
gamma = 0.1
# Ts为抗体持续时间
Ts = 7
# Te为疾病潜伏期
Te = 14
# I_0为感染者的初始人数
I_0 = 1
# E_0为潜伏者的初始人数
E_0 = 0
# R_0为治愈者的初始人数
R_0 = 0
# S_0为易感者的初始人数
S_0 = N - I_0 - E_0 - R_0
# T为传播时间
T = 150

# INI为初始状态下的数组
INI = (S_0,E_0,I_0,R_0)

def funcSEIRS(inivalue,_):
Y = np.zeros(4)
X = inivalue
# 易感个体变化
Y[0] = - (beta * X[0] * X[2]) / N + X[3] / Ts
# 潜伏个体变化
Y[1] = (beta * X[0] * X[2]) / N - X[1] / Te
# 感染个体变化
Y[2] = X[1] / Te - gamma * X[2]
# 治愈个体变化
Y[3] = gamma * X[2] - X[3] / Ts
return Y

T_range = np.arange(0,T + 1)

RES = spi.odeint(funcSEIRS,INI,T_range)

plt.plot(RES[:,0],color = &#39;darkblue&#39;,label = &#39;Susceptible&#39;,marker = &#39;.&#39;)
plt.plot(RES[:,1],color = &#39;orange&#39;,label = &#39;Exposed&#39;,marker = &#39;.&#39;)
plt.plot(RES[:,2],color = &#39;red&#39;,label = &#39;Infection&#39;,marker = &#39;.&#39;)
plt.plot(RES[:,3],color = &#39;green&#39;,label = &#39;Recovery&#39;,marker = &#39;.&#39;)

plt.title(&#39;SEIRS Model&#39;)
plt.legend()
plt.xlabel(&#39;Day&#39;)
plt.ylabel(&#39;Number&#39;)
plt.show()

关于2019-nCoV的SEIR模型参数设置不具备参考性，所以做了删除处理。后续时间可能会更改重新放在这里，也可能更新其他模型（如考虑常量输出输入的SEIR模型、SQIR模型等。。。）
因本人以前从未研究过传染病动力学，只是一时感兴趣，所以不免存在问题，欢迎大家指正～
本文参考的博客链接：
欢迎关注~一个医学生（预防医学）的数据成长之路。。。

氷雪人 · 发表于 2022-12-11 07:56:04

大神求指教运行第五个模型的时候提示没有找到R_0 请问一下这个按照上面提示的输入还是？

任卓 · 发表于 2022-12-11 07:56:49

已经更正代码[赞同]

光荣使命 · 发表于 2022-12-11 07:57:39

最后算出来结果，预测有多少人感染啊

努力更幸福 · 发表于 2022-12-11 07:58:21

因为准确参数无法知道，所以预测人数意义不大，有较大误差。后面再继续更新

我不是大伟 · 发表于 2022-12-11 07:58:34

你好，请教下潜伏期长度与疫情周期有没有关系？

永兴提琴 · 发表于 2022-12-11 07:58:46

SIR模型中的beta = 0.2586，这个数值是怎么确定的？我查了一下资料贝塔的含义：“假设 t 时刻单位时间内，一个病人能传染的易感者数目与此环境内易感者总数s(t)成正比，比例系数为β，从而在t时刻单位时间内被所有病人传染的人数为βs(t)i(t)。”
假设武汉有900万易感人群，每天的感染人数就200多万？贝塔值感觉不会这么大

农民工大毛 · 发表于 2022-12-11 07:59:05

感谢感谢，本文主要着重python实现哈～参数具体并不符合当下情况的～[大笑]

艾则问 · 发表于 2022-12-11 07:59:59

感谢提醒我又仔细看了一下β的定义，它意思是一个病人在t时刻内接触S(t)个人后，这S(t)个人中真正被感染的比例为β。所以真实β值应该在0.2586（参考的是03年香港SARS的β值）附近。[大笑]因为武汉900万人中有很多并没有接触到患者的[大笑]，实际接触到的只是一部分S(t)I(t)（实际接触人数需要去重），而真正最后被感染的是βS(t)I(t)（SIR模型假设每个人只被一个患者接触），而被发现的是小于βS(t)I(t)，被上报的是现在新闻中看到的数字[大笑]这下应该没错了

禁我一言 · 发表于 2022-12-11 08:00:15

这个问题很有意思，刚刚又考虑了一下。潜伏期越长，基本再生数可能越大（见白小鱼的回答），由基本再生数的定义：在发病初期，当所有人均为易感者时，一个病人在其平均患病期内所传染的人数。可知，即β可能越大了，将β带入模型可以得到疫情周期（定义为感染曲线从0开始到0结束的时间）不断减小，潜伏期越长，越不容易被发现，易感人群被感染的越快（表现为感染曲线越陡），所以疫情周期较短。没算相关系数，感兴趣可以算一算，思路是算输出值科学计数法为e-01的两个值区间数与β值之间的相关系数。个人拙见[大笑]我也是菜鸟～

		自动登录	找回密码
密码			立即注册