|
|
传染病的数学模型
近期,国内的疫情闹得沸沸扬扬,很多省市自治区都出现了流感的患者。回想起之前在学校的时候曾经研究过微分方程和动力系统,于是整理一下相关的数学模型,分享给各位读者。笔者并不是研究这个领域的专家,并且这篇文章只是从微分方程角度出发,分析方程的性质,不一定适用于真实环境,而且真实环境比这个也复杂得多。
关于传染病的数学模型,在许多年前数学界早已做过研究,根据传染病的传播速度不同,空间范围各异,传播途径多样,动力学机理等各种因素,对传染病模型按照传染病的类型划分为 SI,SIR,SIRS,SEIR 模型。如果是按照连续时间来划分,那么这些模型基本上可以划分为常微分方程(Ordinary Differential Equation),偏微分方程(Partial Differential Equation)等多种方程模型;如果是基于离散的时间来划分,那么就是所谓的差分方程(Difference Equation)。
在本文中,将会主要介绍常微分方程中的一些传染病数学模型。在介绍方程之前,首先要介绍一些常用的符号:在时间戳 t 上,可以定义以下几种人群:
- 易感者(susceptible):用符号 S(t) 来表示;
- 感染者(infective):用符号 I(t) 来表示;
- 康复者(Recoverd):用符号 R(t) 来表示;
其次,在时间戳 t 上,总人口是 N(t)=S(t)+I(t)+R(t) 。如果暂时不考虑人口增加和死亡的情况,那么 N(t)\equiv N 是一个恒定的常数值。
除此之外,
- r 表示在单位时间内感染者接触到的易感者人数;
- 传染率: \beta 表示感染者接触到易感者之后,易感者得病的概率;
- 康复率:\gamma 表示感染者康复的概率,有可能变成易感者(可再感染),也有可能变成康复者(不再感染)。
在进行下面的分析之前,先讲一个常微分方程的解。
Claim. 假设 x=x(t) 是关于 t 的一个方程,且满足 \frac{dx}{dt} + a_{1}x + a_{2}x^{2}=0 和 x(0)=x_{0} ,那么它的解是: x(t) = \frac{e^{-a_{1}t}}{\frac{1}{x_{0}}-\frac{a_{2}}{a_{1}}(e^{-a_{1}t}-1)} .
Proof. 证明如下:
通过 \frac{dx}{dt}+a_{1}x+a_{2}x^{2}=0 可以得到 -\frac{d}{dt}\bigg(\frac{1}{x}\bigg) + a_{1}\bigg(\frac{1}{x}\bigg)+a_{2}=0 ;令 y = 1/x ,得到 \frac{dy}{dt}-a_{1}y=a_{2} 。所以, \frac{d}{dt}(e^{-a_{1}t}y) = a_{2}e^{-a_{1}t} ,两边积分可以得到 e^{-a_{1}t}y-y_{0}=\bigg(-\frac{a_{2}}{a_{1}}\bigg)(e^{-a_{1}t}-1) ,其中 y_{0}=1/x_{0} 。求解之后得到: x(t) = e^{-a_{1}t}/\bigg(\frac{1}{x_{0}}-\frac{a_{2}}{a_{1}}(e^{-a_{1}t}-1)\bigg) 。
SI 模型(Susceptible-Infective Model)
在 SI 模型里面,只考虑了易感者和感染者,并且感染者不能够恢复,此类病症有 HIV 等;
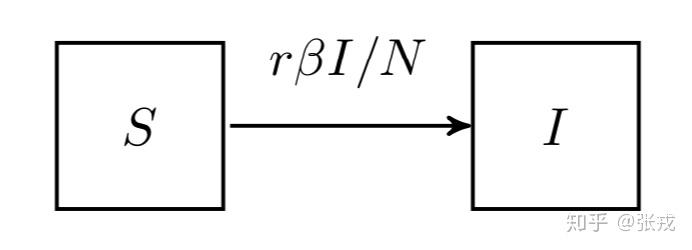
SI Model
其微分方程就是:
\begin{cases}\frac{dS}{dt} = -\frac{r\beta I}{N} S \\ \frac{dI}{dt}=\frac{r\beta I}{N}S \end{cases}
初始条件就是 S(0)=S_{0} , I(0) = I_{0} ,并且 S(t)+I(t)=N 对于所有的 t\geq 0 都成立。
于是,把 S = N - I 代入第二个微分方程可以得到: \frac{dI}{dt} - r\beta I + \frac{r\beta}{N}I^{2}=0 。因此根据前面所提到的常微分方程的解可以得到:
I(t) = \frac{NI_{0}}{I_{0}+(N-I_{0})e^{-r\beta t}} .
这个就是所谓的逻辑回归函数,而在机器学习领域,最简单的逻辑回归函数就是 \sigma(x) = 1/(1+e^{-x}) 这个定义。而 I(t) 只是做了一些坐标轴的平移和压缩而已。由于 \lim_{t\rightarrow +\infty}e^{-t}=0,所以, \lim_{t\rightarrow +\infty}I(t) = N ,从而 \lim_{t\rightarrow +\infty}S(t) = 0 。
通过数值模拟可以进一步知道:
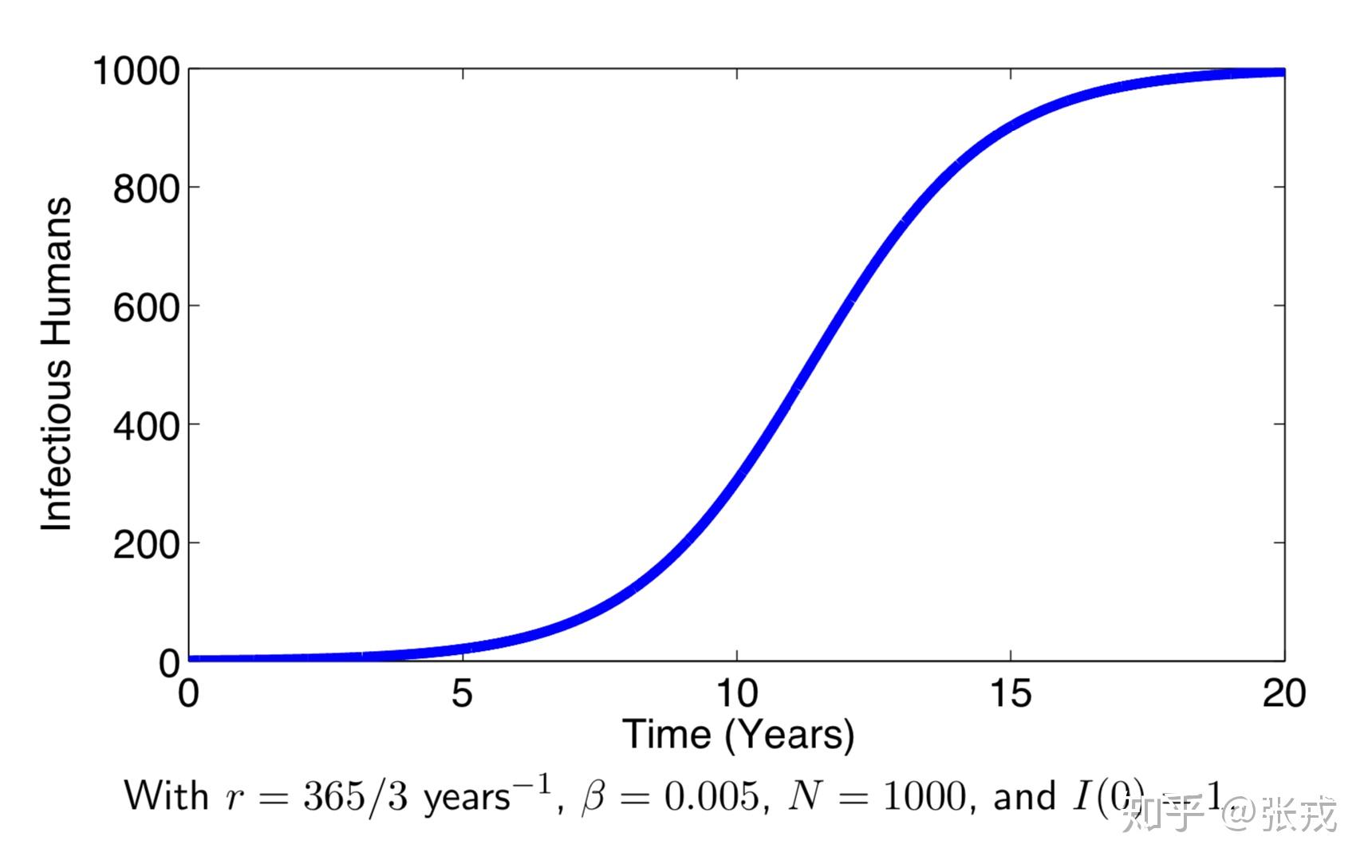
SI model 的数值模拟(一)
简单来看,在 SI 模型的假设下,全部人群到最后都会被感染。
SIS 模型(Susceptible-Infectious-Susceptible Model)
除了 HIV 这种比较严重的病之外,还有很多小病是可以恢复并且反复感染的,例如日常的感冒,发烧等。在这种情况下,感染者就有一定的几率重新转化成易感者。如下图所示:
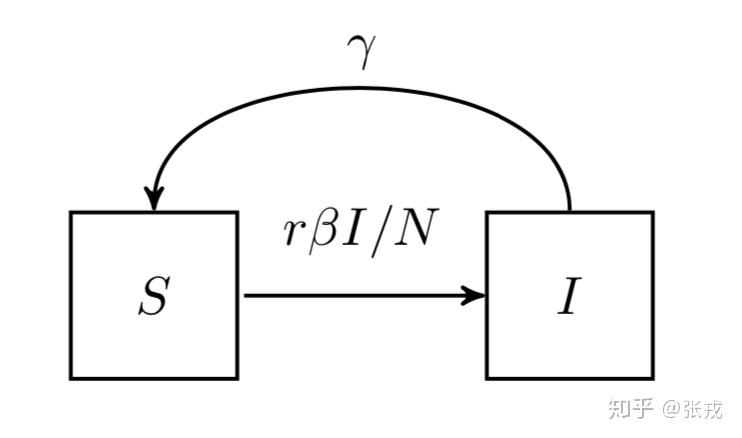
SIS model
其微分方程就是:
\begin{cases} \frac{dS}{dt} = -r \beta S\frac{I}{N} + \gamma I \\ \frac{dI}{dt}=r\beta S \frac{I}{N} - \gamma I \end{cases} ,其初始条件就是 S(0)=S_{0} , I(0)=I_{0} .
使用同样的方法,把 S=N-I 代入第二个微分方程可以得到: \frac{dI}{dt} - (r\beta - \gamma)I + \frac{r\beta}{N}I^{2}=0 . 通过之前的 Claim 可以得到解为:
I(t) = \frac{N(r\beta-\gamma)}{r\beta}/\bigg(\bigg(\frac{N(r\beta-\gamma)}{I_{0}r\beta}-1\bigg)e^{-(r\beta-\gamma)t}+1\bigg) .
从而可以得到 \lim_{t\rightarrow +\infty} I(t) = N(r\beta - \gamma)/(r\beta) 且 \lim_{t\rightarrow +\infty} S(t) = (N\gamma)/(r\beta) . 这个方程同样也是逻辑回归方程,只是它的渐近线与之前的 SI 模型有所不同。
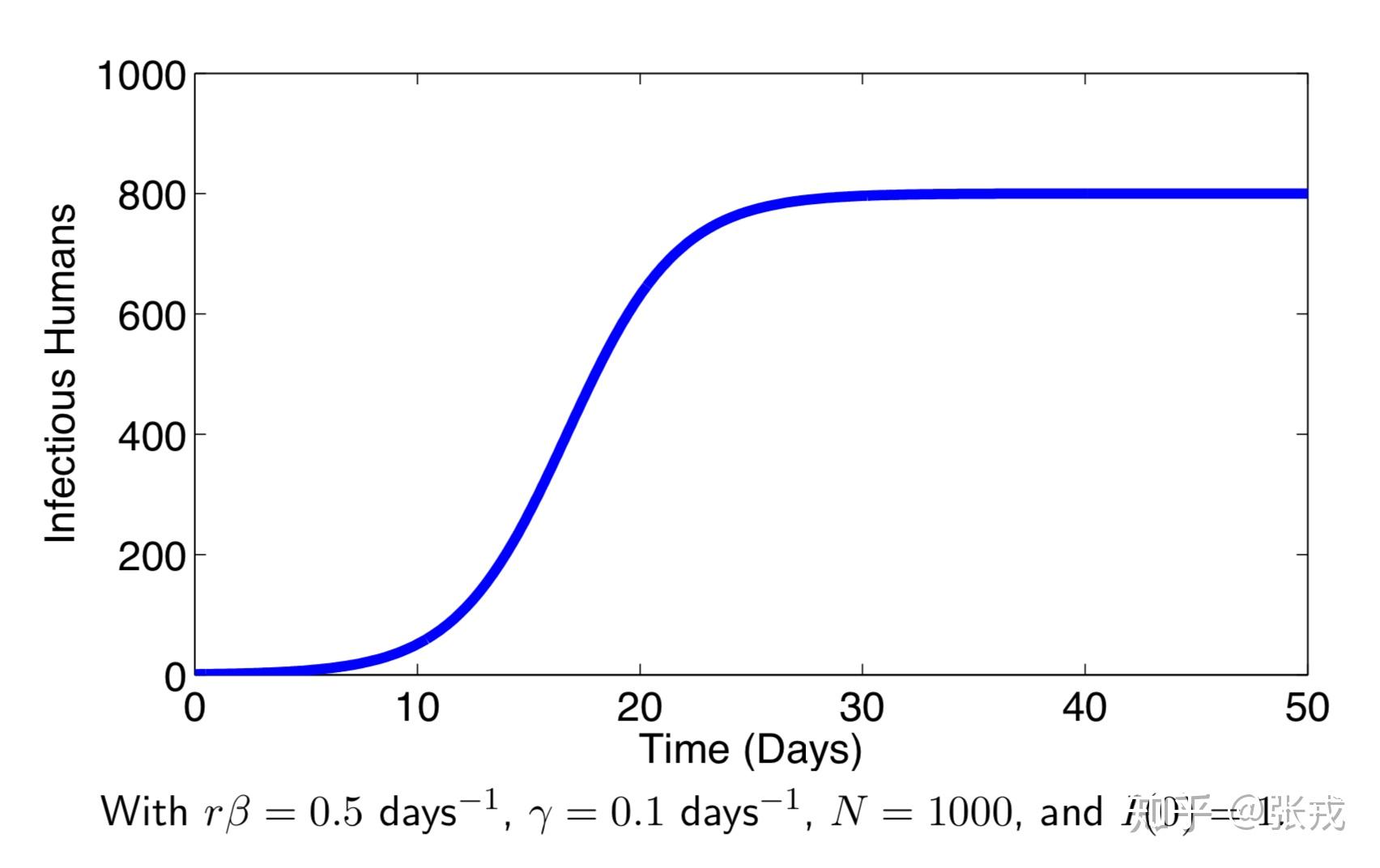
SIS model 的数值模拟(二)
SIR 模型(Susceptible-Infectious-Recovered Model)
有的时候,感染者在康复了之后,就有了抗体,于是后续就不再会获得此类病症,这种时候,考虑 SIS 模型就不合适了,需要考虑 SIR 模型。此类病症有麻疹,腮腺炎,风疹等。
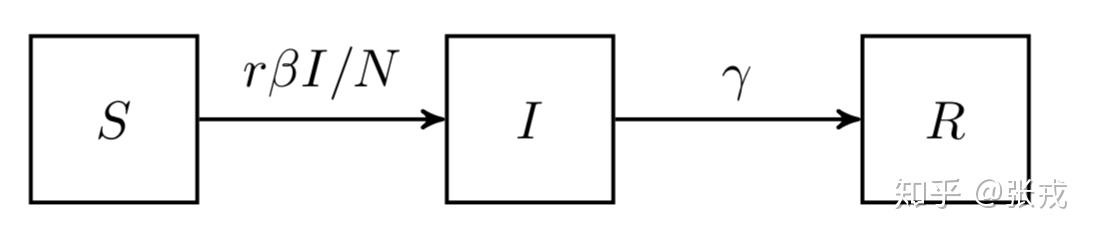
SIR model
其微分方程是: \begin{cases} \frac{dS}{dt}=-r\beta S \frac{I}{N} \\ \frac{dI}{dt}=r\beta S\frac{I}{N} - \gamma I \\ \frac{dR}{dt}=\gamma I\end{cases} 。其初始条件是 S(0)=S_{0}, I(0)=I_{0}, R(0)=R_{0}, 并且 S(t), I(t), R(t)\geq 0 和 S(t) +I(t)+R(t)=N 对于所有的 t\geq 0 都成立。
对于这类方程,就不能够得到其解析解了,只能够从它的动力系统开始进行分析,得到解的信息。根据第一个微分方程可以得到: \frac{dS}{dt} = -r\beta S\frac{I}{N}<0 ,于是 S(t) 是一个严格递减函数。同时, 0\leq S(t)\leq N 对于所有的 t\geq 0 都成立,于是存在 S_{\infty}\in[0,\infty] 使得 \lim_{t\rightarrow \infty}S(t)=S_{\infty} .
通过第一个微分方程和第二个微分方程可以得到: \frac{d(S+I)}{dt} = -\gamma I ,因此对它两边积分得到 \int_{0}^{T} \frac{d(S+I)}{dt} = -\gamma \int_{0}^{T}I(t)dt . 左侧等于 S(T) + I(T) - S(0) - I(0) ,上界是 4N ,因此令 T\rightarrow \infty 可以得到 \int_{0}^{\infty}I(t) dt\leq 4N/\gamma . 而 I(t)\geq 0 且是连续可微函数,因此 \lim_{t\rightarrow \infty}I(t) = 0 。这意味着所有的感染人群都将康复。
由于 S(t) 是严格单调递减函数,因此从第二个微分方程可以得到:当 S(t) = N\gamma/(r\beta) 时,感染人数 I(t) 达到最大值。

SIR model 的数值模拟(一)

SIR model 的数值模拟(二)
其余模型
在以上的 SI,SIS,SIR 模型中,还可以把死亡因素考虑进去。除此之外,还有 SIRS 模型,SEIR 模型等,在这里就不再做赘述。有兴趣的读者可以参阅相关的参考书籍。
参考文献
- Introduction to SEIR Models, Nakul Chitnis, Workshop on Mathematical Models of Climate Variability, Environmental Change and Infectious Diseases, Trieste, Italy, 2017
|
|